Question

Someone solve this for me pls ​

Answer 1

Explanation:

`we \: know \: that \: sum \: of \: angles \: in \: a \: line \: = 180 \\ so \\ x + 31 + x + 20 + x = 180 \\ 3x + 51 = 180 \\ 3x = 180 - 51 \\ 3x = 129 \\ x = (129)/(3) \\ x = 43degree \\ thank \: you`

Answer 2

Answer:-

`\pink{\bigstar}` The measure if ∠x
`\large\leadsto\boxed{\tt\purple{43^(\circ)}}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

• To Find:-

• Measure of
  `\angle` x

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

• Solution:-

The given angles are made by a straight line. We know that the total angle made by a straight line is 180°.

Therefore, all the angles should sum upto 180°.

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

• Working:-

➪
`\sf (x + 31^(\circ)) + (x + 20^(\circ)) + (x) = 180^(\circ)`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

➪
`\sf x + 31^(\circ) + x + 20^(\circ) + x = 180^(\circ)`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

➪
`\sf 3x + 51^(\circ) = 180^(\circ)`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

➪
`\sf 3x = 180^(\circ) - 51^(\circ)`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

➪
`\sf 3x = 129^(\circ)`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

➪
`\sf x = (129)/(3)`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

★
`\large{\bold\red{x = 43^(\circ)}}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

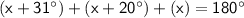
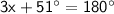
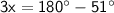
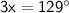
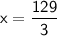
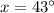
Therefore, the measure of the ∠x is 43°.