Question

A study showed that 25% of the students drive themselves to school. Based on the suggested probability, in a class of 18 students, what would be the probability that at least 6 students drive themselves to school? (CDF)

A) 0.139
B) 0.283
C) 0.717
D) 0.861

Answer 1

B) 0.283

Explanation:

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

25% of the students drive themselves to school.

This means that
`p = 0.25`

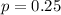
Class of 18 students

This means that
`n = 18`

What would be the probability that at least 6 students drive themselves to school?

This is

`P(X \geq 6) = 1 - P(X < 6)`

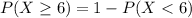
In which

`P(X < 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)`

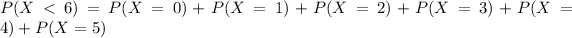
So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(15,0).(0.25)^(0).(0.75)^(18) = 0.006`

`P(X = 1) = C_(15,1).(0.25)^(1).(0.75)^(17) = 0.034`

`P(X = 2) = C_(15,2).(0.25)^(2).(0.75)^(16) = 0.096`

`P(X = 3) = C_(15,3).(0.25)^(3).(0.75)^(15) = 0.17`

`P(X = 4) = C_(15,4).(0.25)^(4).(0.75)^(14) = 0.213`

`P(X = 5) = C_(15,5).(0.25)^(5).(0.75)^(13) = 0.199`

`P(X < 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) = 0.006 + 0.034 + 0.096 + 0.17 + 0.213 + 0.199 = 0.718`

`P(X \geq 6) = 1 - P(X < 6) = 1 - 0.718 = 0.282`

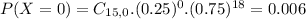
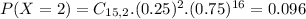
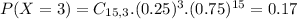
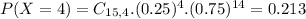
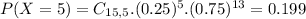
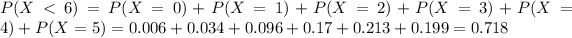
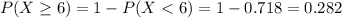
Closest option is B, just a small rounding difference.