Answer:-
 The larger number is
The larger number is

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
• Given:-
- Sum of two numbers is 100.
- Difference between the numbers is 56.
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
• To Find:-
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
• Solution:-
Let the two numbers be 'x' and 'y' respectively.
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
According to the question:-
✯ Sum of two numbers is 100.
➪
![\sf x + y = 100 \dashrightarrow\bold\red{[equation \: 1]}](https://img.qammunity.org/2022/formulas/mathematics/high-school/y4rx42d57soruj9ycpxgr03rcgaid95ydp.png)
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
Also,
✯ Difference between the numbers is 56.
➪
![\sf x - y = 100 \dashrightarrow\bold\red{[equation \: 2]}](https://img.qammunity.org/2022/formulas/mathematics/high-school/zmto2qjtnma9ben0npqwlvierkzer4a4ev.png)
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
• Adding equation [1] and equation [2]:-
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
➪
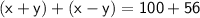
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
➪
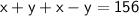
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
➪
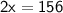
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
➪
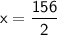
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
★

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
• Substituting the value of x in equation [1]:-
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
➪
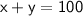
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
➪

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
➪
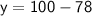
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
★
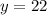
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
Therefore, the numbers are 78 and 22.
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
The larger number is 78.