Answer:
 which implies that C is the integrating factor
which implies that C is the integrating factor
Explanation:
The correct format for the equation given is:
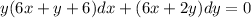
By the application of the general differential equation:
⇒ Mdx + Ndy = 0
where:
M = 6xy+y²+6y
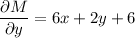
and
N = 6x +2y
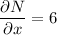
∴
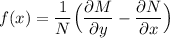
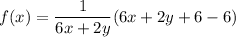
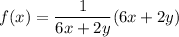
f(x) = 1
Now, the integrating factor can be computed as:
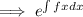
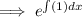
the integrating factor =
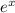
From the given equation:
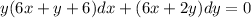
Let us multiply the above given equation by the integrating factor:
i.e.
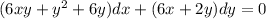
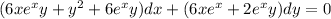
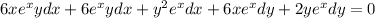
By rearrangement:
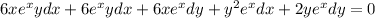
Let assume that:

and:
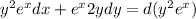
Then:

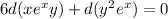
By integration:
 which implies that C is the integrating factor
which implies that C is the integrating factor