Question

1. Mixing Water at Two Temperatures

a. One flask contains 150.0 g water at 20.0 °C. A second flask contains 350.0 g water at 95.0 °C. If the two water samples are mixed, what will the final temperature of the water be?
-Assume that the density of water it 1.000 g/cm^3
-The specific heat capacity for water is 4.184 J/g °C​

Answer 1

`T_f=72.5\°C`

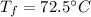
Step-by-step explanation:

Hello!

In this case, since this a problem in which the cold water is heated by the hot water, we can write:

`Q_(hot)+Q_(cold)=0`

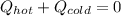
Thus, by plugging in the mass, specific heat and temperatures, we obtain:

`m_(hot)C_(hot)(T_f-T_(hot))+m_(cold)C_(cold)(T_f-T_(cold))=0`

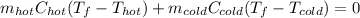
Now, we can also write:

`m_(hot)(T_f-T_(hot))+m_(cold)(T_f-T_(cold))=0`

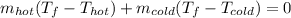
Then, after applying some algebra, it is possible to obtain:

`T_f=(m_(hot)T_(hot)+m_(cold)T_(cold))/(m_(hot)+m_(cold))`

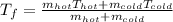
If we plug in, we obtain:

`T_f=(350.0g*95.0\°C+150.0g*20.0\°C)/(350.0g+150.0g)`

`T_f=72.5\°C`

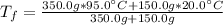
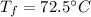
Best regards!