Question

The radius of a circle is 10 cm. What is the approximate area of the circle? What is the exact area of the circle? Show your work.

Answer 1

`\large\boxed{\mathtt{Exact = 100 \pi \ cm^(2)}}`

`\large\boxed{\mathtt{Approximate: 314.16cm^(2)}}`

Explanation:

`\textsf{We are asked to identify the area of the circle with the given radius.}`

`\large\underline{\textsf{What is the Radius?}}`

`\textsf{The \underline{Radius} is a straight \underline{line segment} that covers the distance to the \underline{center} of the}`

`\textsf{circle, to the \underline{circumference}.}`

`\large\underline{\textsf{What is the Formula for Area?}}`

`\textsf{The formula we use for area is;} \mathtt{ \ Area = \pi(radius)^(2).}`

`\textsf{Pi is used to help equal out the ratio of the formula. Mainly, it's helpful to find the area.}`

`\textsf{Now that we have the Radius, we can begin solving.}`

`\Large\underline{\textsf{Substitute:}}`

`\mathtt{Area = \pi(10)^(2)}`

`\mathtt{Area = 100 \pi}`

`\textsf{For our answer,} \ 100 \pi \ \textsf{is the \underline{exact answer} for the area of this circle.}`

`\Large\underline{\textsf{Evalulate 100 pi:}}`

`\mathtt{Area = 100 \pi \approx 314.16cm^(2)}`

`\textsf{314.16cm is the approximate area of this circle.}`

Answer 2

First let's review the area formula for a circle.

Area=π
`r^2`

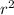
Now that we know the radius, r is 10. The area is

10*10*π=100π

I will approximate π to 3.14 although you could do it more precise or less precise. The final answer will be 100*3.14=314 squared centimeter.

Any question you have about this just ask in the comment of this answer :)