Answer:
Q1:
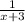
Q2:
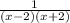
Q3:
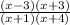
Q4:
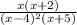
Explanation:
If there is a vertical asymptote at x=k, then the denominator must contain a term (x-k) or (x-k) raised to a positive integer power.
If there is an x intercept at k, then the numerator must contain a term (x-k) or (x-k) raised to a positive integer power.
If there is a horizontal asymptote of 0, then the highest power of x in the denominator must exceed the highest power of x in the numerator.
If thee is a horizontal asymptote of k, then the highest power of x in the numerator and denominator must be the same and the ratio of their coefficients (numerator to denominator) must be k.