Question

Find dy/dx by implicit differentiation for the following equation. e^x^2=7x+5y+3

Answer 1

`\displaystyle (dy)/(dx) = (2e^(2x) - 7)/(5)`

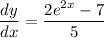
General Formulas and Concepts:

Pre-Algebra

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Exponential Rule [Powering]:
  `\displaystyle (b^m)^n = b^(m \cdot n)`

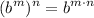
Calculus

Derivatives

Derivative Notation

Derivative of a constant is 0

Implicit Differentiation

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

eˣ Derivative:
`\displaystyle (d)/(dx)[e^u] = u'e^u`

Explanation:

Step 1: Define

`\displaystyle (e^x)^2 = 7x + 5y + 3`

Step 2: Differentiate

1. Rewrite [Exponential Rule - Powering]:
   `\displaystyle e^(2x) = 7x + 5y + 3`
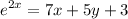
2. Implicit Differentiation:
   `\displaystyle (d)/(dx)[e^(2x)] = (d)/(dx)[7x + 5y + 3]`
3. [Derivative] eˣ derivative:
   `\displaystyle 2e^(2x) = (d)/(dx)[7x + 5y + 3]`
4. [Derivative] Basic Power Rule:
   `\displaystyle 2e^(2x) = 1 \cdot 7x^(1 - 1) + 1 \cdot 5y^(1 - 1)(dy)/(dx)`
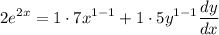
5. [Derivative] Simplify:
   `\displaystyle 2e^(2x) = 7 + 5(dy)/(dx)`
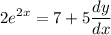
6. [Derivative] [Subtraction Property of Equality] Subtract 7 on both sides:
   `\displaystyle 2e^(2x) - 7 = 5(dy)/(dx)`
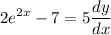
7. [Derivative] [Division Property of Equality] Divide 5 on both sides:
   `\displaystyle (2e^(2x) - 7)/(5) = (dy)/(dx)`
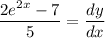
8. [Derivative] Rewrite:
   `\displaystyle (dy)/(dx) = (2e^(2x) - 7)/(5)`

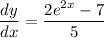
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Derivatives - Implicit Differentiation

Book: College Calculus 10e