Answer:
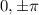
Explanation:
please note that to find but α+β+γ in other words the sum of α,β and γ not α,β and γ individually so it's not an equation
===========================
we want to find all possible values of α+β+γ when tanα+tanβ+tanγ = tanαtanβtanγ to do so we can use algebra and trigonometric skills first
cancel tanγ from both sides which yields:

factor out tanγ:
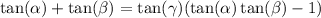
divide both sides by tanαtanβ-1 and that yields:
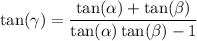
multiply both numerator and denominator by-1 which yields:
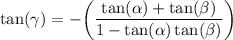
recall angle sum indentity of tan:
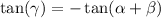
let α+β be t and transform:
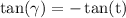
remember that tan(t)=tan(t±kπ) so
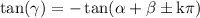
therefore when k is 1 we obtain:
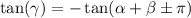
remember Opposite Angle identity of tan function i.e -tan(x)=tan(-x) thus
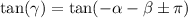
recall that if we have common trigonometric function in both sides then the angle must equal which yields:
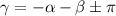
isolate -α-β to left hand side and change its sign:
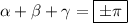
when is 0:
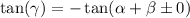
likewise by Opposite Angle Identity we obtain:
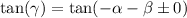
recall that if we have common trigonometric function in both sides then the angle must equal therefore:
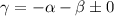
isolate -α-β to left hand side and change its sign:
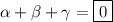
and we're done!