Question

Steel wire rope is used to lift a heavy object. We use a 3.1m steel wire that

is 6.0mm in diameter and lift a 1700kg object. Then, the wire elongates
0.17m. Calculate the Young’s modulus for the rope material.

Answer 1

Young's modulus for the rope material is 20.8 MPa.

Step-by-step explanation:

The Young's modulus is given by:

`E = (FL_(0))/(A\Delta L)`

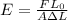
Where:

F: is the force applied on the wire

L₀: is the initial length of the wire = 3.1 m

A: is the cross-section area of the wire

ΔL: is the change in the length = 0.17 m

The cross-section area of the wire is given by the area of a circle:

`A = \pi r^(2) = \pi ((0.006 m)/(2))^(2) = 2.83 \cdot 10^(-5) m^(2)`

Now we need to find the force applied on the wire. Since the wire is lifting an object, the force is equal to the tension of the wire as follows:

`F = T_(w) = W_(o)`

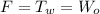
Where:

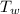`T_(w)`: is the tension of the wire

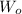`W_(o)`: is the weigh of the object = mg

m: is the mass of the object = 1700 kg

g: is the acceleration due to gravity = 9.81 m/s²

`F = mg = 1700 kg*9.81 m/s^(2) = 16677 N`

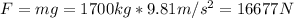
Hence, the Young's modulus is:

`E = (16677 N*0.006 m)/(2.83 \cdot 10^(-5) m^(2)*0.17 m) = 20.8 MPa`

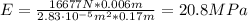
Therefore, Young's modulus for the rope material is 20.8 MPa.

I hope it helps you!