Answer:
The the linear speed (in m/s) of a point on the rim of this wheel at an instant=0.418 m/s
Step-by-step explanation:
We are given that
Angular acceleration,
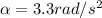
Diameter of the wheel, d=21 cm
Radius of wheel,
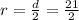 cm
cm
Radius of wheel,
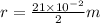
1m=100 cm
Magnitude of total linear acceleration, a=
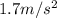
We have to find the linear speed of a at an instant when that point has a total linear acceleration with a magnitude of 1.7 m/s2.
Tangential acceleration,
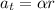
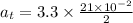
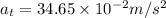
Radial acceleration,
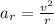
We know that
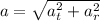
Using the formula
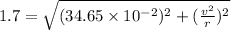
Squaring on both sides
we get

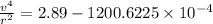
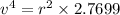
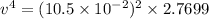

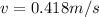
Hence, the the linear speed (in m/s) of a point on the rim of this wheel at an instant=0.418 m/s