Question

The 2nd maximum of a double slit diffraction pattern makes an angle 20 degrees when a wavelength of 600 nm is used. What is the angle for the 5th maximum when the slit separation d is increased to 1.5d keeping the wavelength the same. g

Answer 1

θ = 34.77°

Step-by-step explanation:

From diffraction equation:

`m\lambda = dSin\theta`

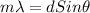
where,

m = order of diffraction

λ = wavelength of light used

d = slit separation

θ = angle

Therefore, for initial case:

m = 2

λ = 600 nm = 6 x 10⁻⁷ m

d = slit seperation = ?

θ = angle 20°

Therefore,

`(2)(6\ x\ 10^(-7)\ m)=d(Sin\ 20^o)\\\\d = (12\ x 10^(-7)\ m)/(0.342)\\\\d = 3.5\ x\ 10^(-6)\ m`

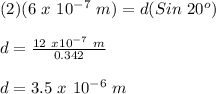
Now, for the second case:

m = 5

λ = 600 nm = 6 x 10⁻⁷ m

d = slit seperation = (1.5)(3.5 x 10⁻⁶ m) = 5.26 x 10⁻⁶ m

θ = angle = ?

Therefore,

`(5)(6\ x\ 10^(-6)\ m) = (5.26\ x\ 10^(-6)\ m)Sin\theta\\\\Sin\theta = ((5)(6\ x\ 10^(-7)\ m))/((5.26\ x\ 10^(-6)\ m))\\\\\theta = Sin^(-1)(0.5703)`

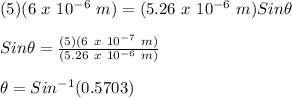
θ = 34.77°