Answer:
A two-variable function is something like:
z = f(x, y).
We want this function to not be continuous at (1, 2), this means that x = 1 and y = 2.
Now, a easy way to make a function not continuous at a given point, we can have a denominator that is equal to zero at that particular point, and this is because we can not divide by zero
For example, we could have:
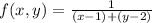
The denominator is (x - 1) + (y - 2)
When x = 1, and y = 2, this is equal to zero, then this function is not continuous in the point (1, 2).