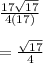Question

How to rationalize
`(17)/(4√(1)7 )`? Please explain.

Answer 1

`(√(17))/(4)`

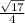
Explanation:

Rationalizing the denominator of a fraction is when one multiplying fraction such that it removes any radical from the denominator. This can be done by multiplying both the numerator and the denominator by the radical that is present in the denominator. In fractional terms, a number over itself is equal to one, therefore, doing this would keep the equation true. After multiplying, one will simplify the resulting fraction.

`(17)/(4√(17)) * (√(17))/(√(17))\\\\= (17√(17))/(4(17))\\`

Simplify like factor found in both the numerator and the denominator,

`(17√(17))/(4(17))\\\\= (√(17))/(4)`