Question

Ou roll a fair 666-sided die. What is \text{P(not 5})P(not 5)start text, P, left parenthesis, n, o, t, space, 5, end text, right parenthesis? If necessary, round your answer to 222 decimal places.

Answer 1

Explanation:

its 0.83 i did it on kahn

Answer 2

Given:

A 6 sided die is rolled.

To find:

The probability of getting not 5, i.e., P( not 5).

Solution:

If a 6 sided die is rolled, then the possible outcomes are 1, 2, 3, 4, 5, 6.

Total outcomes = 6

Favorable outcomes = Possible numbers other than 5 = 5

Now,

`P(\text{ not 5})=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

`P(\text{ not 5})=(5)/(6)`

`P(\text{ not 5})=0.8333...`

`P(\text{ not 5})\approx 0.83`

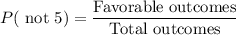
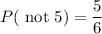
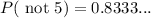
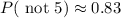
Therefore, the probability of getting not 5, i.e., P( not 5) is 0.83.