Given:
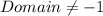
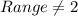
To find:
The function for the given domain and range.
Solution:
A function is not defined for some values that makes the denominator equals to 0.
The denominator of functions in option A and C is
 .
.
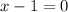
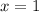
So, the functions in option A and C are not defined for
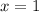 but defined for
but defined for
 . Therefore, the options A and C are incorrect.
. Therefore, the options A and C are incorrect.
In option B, the denominator is equal to
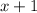 .
.
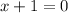

So, the function is not defined for
 . Thus,
. Thus,
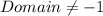 .
.
If degree of numerator and denominator are equal then the horizontal asymptote is
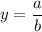 , where a is the leading coefficient of numerator and b is the leading coefficient of denominator.
, where a is the leading coefficient of numerator and b is the leading coefficient of denominator.
In option B, the leading coefficient of numerator is 2 and the leading coefficient of denominator is 1. So, the horizontal asymptote is:
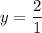
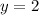
It means, the value of the function cannot be 2 at any point. So,
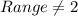 .
.
Hence, option B is correct.