Question

A simple pendulum takes 2.00 s to make one compete swing. If we now triple the length, how long will it take for one complete swing

Answer 1

3.464 seconds.

Step-by-step explanation:

We know that we can write the period (the time for a complete swing) of a pendulum as:

`T = 2*\pi*\sqrt{(L)/(g) }`

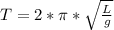
Where:

`\pi = 3.14`

L is the length of the pendulum

g is the gravitational acceleration:

g = 9.8m/s^2

We know that the original period is of 2.00 s, then:

T = 2.00s

We can solve that for L, the original length:

`2.00s = 2*3.14*\sqrt{(L)/(9.8m/s^2) }\\\\(2s)/(2*3.14) = \sqrt{(L)/(9.8m/s^2)}\\\\((2s)/(2*3.14))^2*9.8m/s^2 = L = 0.994m`

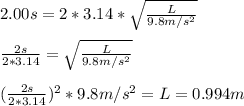
So if we triple the length of the pendulum, we will have:

L' = 3*0.994m = 2.982m

The new period will be:

`T = 2*3.14*\sqrt{(2.982m)/(9.8 m/s^2) } = 3.464s`

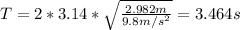
The new period will be 3.464 seconds.