Work Energy Theorem :-
- It states that net work done on any body is equal to the change in its kinetic energy .
We could derive this , as ;
- Consider a body of mass m being pushed by a force F acting along the horizontal , due to which it is displaced s m away .
- Since the angle between the force and the displacement is 0° , work done will be ,
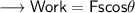
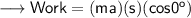
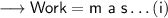
- Now let's use the third equation of motion namely,
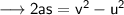
where the symbols have their usual meaning.
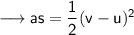
Multiplying both sides by m,
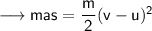
Now from equation (i),
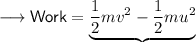
Above term on RHS is change in the Kinetic energy , therefore ,
