Question

If an object free-falls for t seconds from rest to d distance, how far will the object fall from rest in twice the elapsed time?

Answer 1

When the time of fall is doubled, the height of fall will be quadrupled

Step-by-step explanation:

Given;

height of fall, h = d m

time of fall, t = t s

initial velocity of the object, u = 0 m/d

The height of fall of the object is calculated from the kinematic equation below;

`h = ut + (1)/(2) gt^2\\\\h = 0 + (1)/(2) gt^2\\\\h = (1)/(2) gt^2\\\\2h = gt^2\\\\g = (2h)/(t^2)`

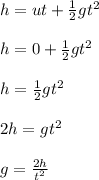
where;

g is acceleration due to gravity, which is constant

if the time of fall is doubled, the height of fall is calculated as;

`(2h_1)/(t_1^2) = (2h_2)/(t_2^2) \\\\(h_1)/(t_1^2) = (h_2)/(t_2^2)\\\\(Note: h_1 = d, \ and \ t_1 = t)\\\\h_2 = (h_1t_2^2)/(t_1^2) \\\\h_2 = ((d)(2t_1)^2)/(t_1^2) \\\\h_2 = ((d)(2t)^2)/(t^2)\\\\h_2 = ((d)* 4t^2)/(t^2)\\\\h_2 = 4d`

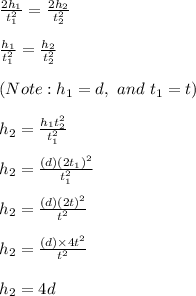
Therefore, when the time of fall is doubled, the height of fall will be quadrupled