Question

You and a friend start riding bikes toward

each other from opposite ends of a 24-mile biking route. you
ride 2 1/6 miles every 1/4 hour . your friend rides 7 1/3 miles per hour.
a. after how many hours do you meet?
b. when you meet, who has traveled farther? how much farther? ​

Answer 1

1.5 hours

I traveled farther

2 miles

Explanation:

`\text{Speed}=\frac{\text{Distance}}{\text{Time}}`

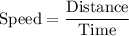
My speed

`(2(1)/(6))/((1)/(4))=((13)/(6))/((1)/(4))=(26)/(3)\ \text{mph}`

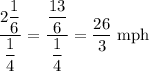
Speed of my friend

`7(1)/(3)=(22)/(3)\ \text{mph}`

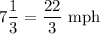
Time passed for both me and my friend will be equal if we start at the same time and the combined distance covered by both of us will be 24 miles. Let
`t` be the time taken to meet

`\text{Distance}=\text{Speed}*\text{Time}`

`(26)/(3)t+(22)/(3)t=24\\\Rightarrow (48)/(3)t=24\\\Rightarrow 16t=24\\\Rightarrow t=(24)/(16)\\\Rightarrow t=1.5\ \text{hours}`

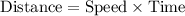
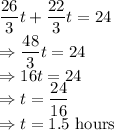
So, we meet each other after 1.5 hours.

Distance traveled by me

`(26)/(3)* 1.5=13\ \text{miles}`

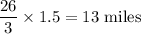
Distance traveled by my friend

`(22)/(3)* 1.5=11\ \text{miles}`

So, I traveled farther by
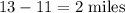`13-11=2\ \text{miles}`.