Question

NO LINKS!!!!

Answer each question below. For each question, draw a diagram and label each side of the triangle with a,b, or c. Also, write the correct give measurements on the sides of the triangle.

1. A 25-foot ladder is leaned against the wall. If the base of the ladder is 7 feet from the wall, how high up the wall will the ladder reach?


2. Two jets leave the airport at the same time. One jet travels east at 300 miles per hour. The other jet travels south at 400 miles per hour. How far apart will the jets be at the end of one hour?


3. As you swim across an 80-meter river, the current carries you 30 meters downstream. How far do you actually swim?

Answer 1

The diagrams are shown below.

======================================================

Problem 1

We have a right triangle with horizontal leg
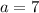`a = 7` and hypotenuse
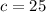`c = 25` to represent the length of the ladder. Use the pythagorean theorem to find the vertical leg b.

`a^2+b^2 = c^2\\\\7^2+b^2 = 25^2\\\\49+b^2 = 625\\\\b^2 = 625-49\\\\b^2 = 576\\\\b = √(576)\\\\b = 24`

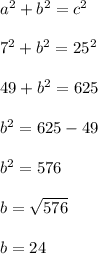
Answer: 24 feet

======================================================

Problem 2

After 1 hour, the first jet has traveled 300 miles while the other has traveled 400 miles. Use the formula

`\text{distance = rate*time}`

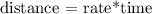
We'll have a right triangle with the two legs of
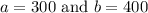`a = 300 \text{ and } b = 400`. The order of 'a' and b doesn't matter.

Use the pythagorean theorem to find the hypotenuse c.

`a^2+b^2 = c^2\\\\c = √(a^2+b^2)\\\\c = √(300^2+400^2)\\\\c = √(90,000 + 160,000)\\\\c = √(250,000)\\\\c = 500\\\\`

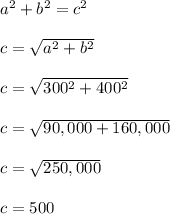
The two jets are 500 miles apart after one hour.

Answer: 500 miles

======================================================

Problem 3

We have a right triangle with horizontal leg 80 meters and vertical leg 30 meters. The hypotenuse is the distance you travel.

`a^2+b^2 = c^2\\\\c = √(a^2+b^2)\\\\c = √(30^2+80^2)\\\\c = √(900+6400)\\\\c = √(7300)\\\\c = √(100*73)\\\\c = √(100)*√(73)\\\\c = 10√(73)\\\\c \approx 85.440037`

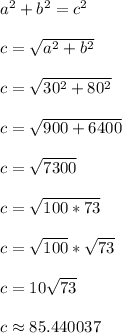
Exact Answer:
`\boldsymbol{10√(73)}` meters

Approximate answer: 85.440037 meters