Answer:
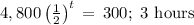
Explanation:
Every hour, the research assistant is removing half the mass from the original 4,800 micrograms of the bacteria culture. So, the mass remaining after t hours can be represented by an exponential expression, a(b)t, where a is the initial mass of the bacteria culture and b is the base of the exponent that represents the decay factor. Since half of the mass of bacteria is being removed every hour, half of the mass remains. So, b =
 . The exponential expression for this situation is
. The exponential expression for this situation is
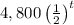 .
.
The research assistant will stop removing half the mass from the original bacteria culture after the original bacteria culture has a mass of 300 micrograms. Hence, set the expression for the mass remaining after t hours equal to 300.
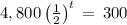
In order to solve this equation for t, the base needs to be isolated. Divide both sides of the inequality by 4,800.
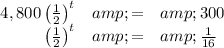
Next, rewrite the base of
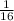 as a power of
as a power of
 . Then, set the exponents equal to each other to solve for t.
. Then, set the exponents equal to each other to solve for t.
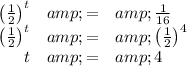
So, after 4 hours the research assistant will stop removing half the mass of the bacteria culture.