Question

441,457 views

2 Answers

Dejan Toteff · Answer 1 · 2022-08-19T04:17:43+0000

Answer:

Considering an standard significance level of 0.05.

The p-value of the test is the probability of finding a sample proportion above 0.1, which is 1 subtracted by the p-value of z = 1.37.

Looking at the z-table, z = 1.37 has a p-value of 0.9147

1 - 0.9147 = 0.0853

The p-value of the test is 0.0853 > 0.05, which means that there is not enough evidence to reject the manufacturer's claim based on this observation.

Explanation:

SupAl · Answer 2 · 2022-08-23T03:19:55+0000

Answer:

The p-value of the test is 0.0853 > 0.05, which means that there is not enough evidence to reject the manufacturer's claim based on this observation.

Explanation:

A manufacturer of nails claims that only 4% of its nails are defective.

At the null hypothesis, we test if the proportion is of 4%, that is:

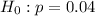
H_0: p = 0.04

At the alternative hypothesis, we test if the proportion is more than 4%, that is:

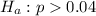
H_a: p > 0.04

The test statistic is:

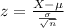
$z = (X - \mu)/((\sigma)/(√(n)))$

In which X is the sample mean,
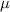$\mu$ is the value tested at the null hypothesis,
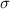$\sigma$ is the standard deviation and n is the size of the sample.

4% is tested at the null hypothesis

This means that
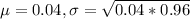
$\mu = 0.04, \sigma = √(0.04*0.96)$

A random sample of 20 nails is selected, and it is found that two of them, 10%, are defective.

This means that
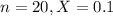
n = 20, X = 0.1

Value of the test statistic:

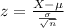
$z = (X - \mu)/((\sigma)/(√(n)))$

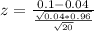
z = (0.1 - 0.04)/((√(0.04*0.96))/(√(20)))

z = 1.37

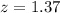
P-value of the test and decision:

Considering an standard significance level of 0.05.

The p-value of the test is the probability of finding a sample proportion above 0.1, which is 1 subtracted by the p-value of z = 1.37.

Looking at the z-table, z = 1.37 has a p-value of 0.9147

1 - 0.9147 = 0.0853

The p-value of the test is 0.0853 > 0.05, which means that there is not enough evidence to reject the manufacturer's claim based on this observation.

Your comment on this question: