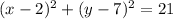Question

Find the standard form of the equation of the circle with endpoints of a diameter at the points (7,8) and (-3,6). Type the standard form of the equation of this circle​

Answer 1

The equation of the circle is
`(x - 2)^2 + (y - 7)^2 = 21`

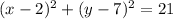
Explanation:

Equation of a circle:

The equation of a circle, with center
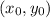`(x_0,y_0)` and radius r is given by:

`(x - x_0)^2 + (y - y_0)^2 = r^2`

Distance between two points:

Suppose that we have two points,
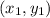`(x_1,y_1)` and
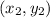`(x_2,y_2)`. The distance between them is given by:

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

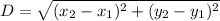
Diameter at the points (7,8) and (-3,6).

The diameter is the distance between these two points, so:

`D = √((-3-7)^2+(6-8)^2) = √(104)`

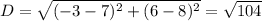
Radius is half the diameter, so:

`r = (√(104))/(2) = (√(104))/(√(4)) = \sqrt{(104)/(4)} = √(21)`

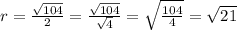
So

`r^2 = (√(21))^2 = 21`

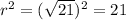
Center:

Midpoint of the diameter, which is the mean of the coordinates. So

`x_0 = (7 - 3)/(2) = (4)/(2) = 2`

`y_0 = (8 + 6)/(2) = (14)/(2) = 7`

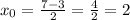
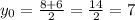
Then

`(x - 2)^2 + (y - 7)^2 = 21`