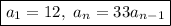Answer:
D. a[1] = 12; a[n] = 33·a[n-1]
Explanation:
You can make the correct choice by seeing what you get with n=1 and n=2 in the various expressions.
In general,
an = a1·r^(n-1)
For n=1, the value of this is ...
a1 = a1·r^(1-1) = a1·r^0 = a1 . . . . as you expect.
That is, the a1 term of the recursive formula is the leading coefficient in the explicit formula.
__
For n=2, you have ...
a2 = a1·r(2-1) = a1·r
That is, the previous term was multiplied by r. In the given explicit formula, r=33, so the recursive formula will tell you ...
a[n] = 33·a[n-1]
__
Altogether, we have ...