Question

PLEASE HELP!!

(-1,3) and (-3,1) as a slope intercept form.

Answer 1

Answer: y = x + 4

===============================================

Step-by-step explanation

The first step is to compute the slope.

`(x_1,y_1) = (-1,3) \text{ and } (x_2,y_2) = (-3,1)\\\\m = \text{slope} = \frac{\text{rise}}{\text{run}} = \frac{\text{change in y}}{\text{change in x}}\\\\m = \frac{\text{y}_(2) - \text{y}_(1)}{\text{x}_(2) - \text{x}_(1)}\\\\m = (1 - 3)/(-3 - (-1))\\\\m = (1 - 3)/(-3 + 1)\\\\m = (-2)/(-2)\\\\m = 1\\\\`

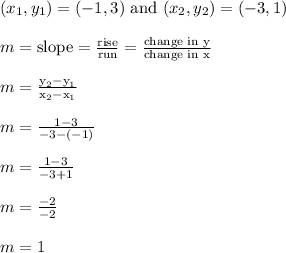
Now apply point-slope form.

`\text{y} - \text{y}_1 = \text{m}(\text{x}-\text{x}_1)\\\\\text{y} - 3 = 1(\text{x}-(-1))\\\\\text{y} - 3 = \text{x}+1\\\\\text{y} = \text{x}+1+3\\\\\text{y} = \text{x}+4\\\\`

The final answer is y = x + 4

It's in the form y = mx+b

m = 1 = slope

b = 4 = y intercept

--------

As a check, plug in x = -1 to get...

y = x+4

y = -1+4

y = 3

This confirms (-1,3) is on the line.

Now check x = -3

y = x+4

y = -3+4

y = 1

We have confirmed (-3,1) is also on the line. The answer overall is confirmed.

Graphing tools like GeoGebra and Desmos can be used to quickly verify the answer.

Side note: y = x+4 converts to x-y = -4