Question

Four congruent circles are inscribed in a square with a side length of 28. if a point in the square is chosen at random, what is the probability that the point is not in a circle?

Answer 1

The probability that a randomly chosen point in a square inscribed with four congruent circles with a side length of 28 units is not in a circle is approximately 21.44% (rounded to four decimal places).

To find the probability that a randomly chosen point in the square is not in a circle, we first need to calculate the area of the square and the combined area of the four congruent circles, and then use these values to determine the probability.

Here are the steps to calculate it:

Step 1: Find the area of the square.

The square has a side length of 28 units. So, its area
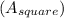`(A_(square) )` is given by:

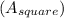`(A_(square) )` = side length × side length = 28 × 28 = 784 square units.

Step 2: Find the radius of one of the congruent circles.

Since there are four congruent circles inscribed in the square, we can divide the square into four equal squares, each containing one of the circles. To find the radius of one of these circles, we need to calculate the side length of one of these smaller squares.

Each smaller square has half the side length of the large square, so:

Side length of smaller square = 28 / 2 = 14 units.

Now, the radius of one of the circles is equal to half the side length of the smaller square, so:

Radius of one circle (r) = 14 / 2 = 7 units.

Step 3: Find the area of one circle.

The area of a circle is given by the formula:

`A__(circle)` = π × r^2, where r is the radius.

Substituting the radius we found:

`A__(circle)` = π × (7^2) = π × 49 = 49π square units.

Step 4: Find the combined area of four circles.

Since there are four congruent circles, the combined area of these circles is:

Combined area of circles = 4 ×
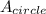`A_(circle)` = 4 × (49π) = 196π square units.

Step 5: Find the area not covered by the circles.

To find the area not covered by the circles, subtract the combined area of the circles from the area of the square:

Area not covered by circles =
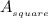`A__(square)` - Combined area of circles = 784 - 196π square units.

Step 6: Calculate the probability.

To find the probability that a randomly chosen point is not in a circle, divide the area not covered by circles by the total area of the square:

Probability = (Area not covered by circles) / (Area of square)

Probability = (784 - 196π) / 784

Now, you can calculate this value numerically:

Probability ≈ (784 - 196 × 3.14159) / 784 ≈ (784 - 615.75244) / 784 ≈ 168.24756 / 784 ≈ 0.2144 (rounded to four decimal places).

So, the probability that a randomly chosen point in the square is not in a circle is approximately 0.2144, or 21.44%.