The probability of having fewer than 3 twins in a random sample of 100 American births, where the twin birth rate is 2%, is approximately 0.6478. This calculation uses the binomial probability formula to find the cumulative probability of 0, 1, or 2 twin births.
To find the probability that less than 3 of the 100 births resulted in twins, we can use the binomial probability formula. In this case, we have a binomial distribution with the following parameters:
Probability of success (having twins): p = 0.02 (2% or 0.02 as a decimal).
Number of trials (sample size): n = 100.
We want to find P(X < 3), where X is the number of births resulting in twins.
To find P(X < 3), we need to calculate P(X = 0) + P(X = 1) + P(X = 2). You can calculate each of these probabilities using the binomial probability formula:
P(X = k) = C(n, k) *
 *
*
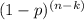
Where:
C(n, k) is the binomial coefficient, which represents the number of ways to choose k successes out of n trials and is calculated as C(n, k) = n! / (k! * (n - k)!).
p is the probability of success.
k is the number of successes we're interested in.
n is the number of trials.
Now, let's calculate each of these probabilities step by step:
Step:1 P(X = 0):
P(X = 0) = C(100, 0) * (0.02)^0 * (1 - 0.02)^(100 - 0)
P(X = 0) = 1 * 1 * 0.98^100 ≈ 0.1326 (rounded to four decimal places)
Step:2 P(X = 1):
P(X = 1) = C(100, 1) * (0.02)^1 * (1 - 0.02)^(100 - 1)
P(X = 1) = 100 * 0.02 * 0.98^99 ≈ 0.2707 (rounded to four decimal places)
Step:3 P(X = 2):
P(X = 2) = C(100, 2) * (0.02)^2 * (1 - 0.02)^(100 - 2)
P(X = 2) = 4950 * 0.02^2 * 0.98^98 ≈ 0.2445 (rounded to four decimal places)
Now, add these probabilities together to find the probability that less than 3 of the 100 births resulted in twins:
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)
P(X < 3) ≈ 0.1326 + 0.2707 + 0.2445 ≈ 0.6478
So, the probability that less than 3 of the 100 births resulted in twins is approximately 0.6478 (rounded to four decimal places).