1. V = 560.00 cm
Here is the answer for the volume of the trapezoidal prism.
We make two rectangular prisms out of the shape, or a rectangular prism and two triangles.
For this case, I'll just do the two prisms.
Here is the formula for volume we'll be using.
V = lwh (shape's volume = length × width × height), or
V = bh (shape's volume = base area × height)
A reference of the rectangular prism can be identified because the length of the horizontal crest is marked at 8 centimeters.
Following V = lwh, we already have the length we need.
The width of the reference prism that doesn't include the diagonal triangular prisms is 10 centimeters.
l = 8 cm
w = 10 cm
And as indicated by the line inside,
h = 4 cm
We'll label this first volume calculation V
 .
.
V
 = 8 cm × 10 cm × 4 cm
= 8 cm × 10 cm × 4 cm
Now for the second volume.
Since two congruent right triangular prisms can come together to equal a second rectangular prism whose volume is two times their original shapes, we can use the same formula
V = lwh
And in order to determine what values are needed, we
- subtract the length of the trapezoid's base from the rectangular prism's.
And that's it. No adjustments are made in the width or height. Those measurements are equal to the reference rectangular prism (center prism).
14 cm - 8 cm = 6 cm
l = 6 cm
w = 10 cm
h = 4 cm
This part of the enumeration will be V
 .
.
V
 = 6 cm × 10 cm × 4 cm
= 6 cm × 10 cm × 4 cm
V
 + V
+ V
 = V
= V
 , or the actual volume of the trapezoidal prism.
, or the actual volume of the trapezoidal prism.
(8 cm × 10 cm × 4 cm) + (6 cm × 10 cm × 4 cm) = 320 cm + 240 cm = 560 cm.
You round to 2 decimal places, so V
 = 560.00 cm.
= 560.00 cm.
2. x = 0.45
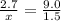
Let's look at the right side.
9.0, or 9, divided by 1.5 equals 6.
Now your equation looks like
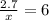
You want to get the variable x by itself so that there aren't any real number values that stop the proportion from being simplified.
So, we multiply x on both sides.
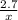 *
*
 =
=
 *
*

On the left side of the = sign, the x on the denominator is being cancelled out.
Now it looks like
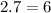 *
*

Divide 6 from both sides to cancel the 6 from the right side and get the new value of x by itself.
2.7 ÷ 6 = 0.45
0.45 is already in the hundredths, so there's no need to round up or down.
3. Height of tree = 19.5 ft
All you have to do here is find the ratios of the two figures to their shadows.
It's going to look like the
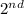 problem because all we're doing is finding the missing variable.
problem because all we're doing is finding the missing variable.
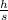 will represent the height-shadow ratio.
will represent the height-shadow ratio.
For a 6.5-foot human to cast a 1.8-foot shadow,
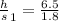
6.5 ft ÷ 1.8 ft ≅ 3.611
All we have to do now is find a tree height that divides by its shadow, 5.4, to get roughly 3.611.
We can solve that by multiplying 3.611 with the shadow's height.
3.611 * 5.4 = 19.5
The tree is 19.5 feet tall.
4. x = 43.6
These two triangles aren't congruent, but similar.
Like the last two problems, finding the ratio between the sides is key to solving the problems.
This time, the ratios of the two given sides for each triangle will let us solve the side-side-side (SSS) rule, if we take it a step further and use the Pythagorean Theorem. For now, just solve the target of the problem.
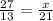
27 ÷ 13 = 2.077
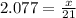
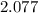 * 21 =
* 21 =
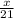 * 21
* 21
Cancel the 21s from the denominator and factor on the right side.
43.617 = x
x = 43.6 because you round to one decimal.