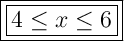Answer:
4 ≤ x ≤ 6
Explanation:
To solve the compound inequality, solve each part of the inequality separately and then find the values of x that satisfy both inequalities.
Solve the left inequality:

So, the solution to the left inequality is x ≥ 4.
Solve the right inequality:
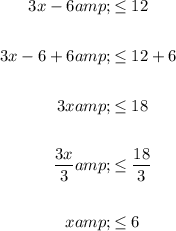
So, the solution to the right inequality is x ≤ 6.
Now, we need to find the values of x that satisfy both inequalities simultaneously, which means we are looking for the intersection of the solutions.
Since x must be greater than or equal to 4 (x ≥ 4) and less than or equal to 6 (x ≤ 6), the common solution is 4 ≤ x ≤ 6.
So, the solution to the compound inequality 2 + x ≤ 3x − 6 ≤ 12 is: