Question

Triangle QRS has coordinates R(-6,9) and S(4,19). What coordinates of point Q will give the triangle a perimeter of 39.1?

Answer 1

the coordinates of point Q that give triangle QRS a perimeter of approximately 39.1 units are (-12, 15), which corresponds to option A. This is the result after carefully calculating the distance for each option and summing them to find the perimeter that matches the given requirement.

We will calculate the distance of side RS and then check each of the options (A, B, C, D) to see which one gives a total perimeter of approximately 39.1 units for the triangle QRS.

**Step 1: Calculate the length of side RS**

We use the distance formula between two points
`\( (x_1, y_1) \)` and
`\( (x_2, y_2) \)` given by:

`\[ d = √((x_2 - x_1)^2 + (y_2 - y_1)^2) \]`

For points R(-6,9) and S(4,19), the length of side RS is:

`\[ RS = √((4 - (-6))^2 + (19 - 9)^2) \]`

`\[ RS = √((4 + 6)^2 + (19 - 9)^2) \]`

`\[ RS = √(10^2 + 10^2) \]`

`\[ RS = √(200) \]`

`\[ RS = 10√(2) \]`

The exact value of
`\( RS \)` is
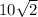`\( 10√(2) \)`, which we will approximate to two decimal places as part of the calculations.

Step 2: Calculate QR and QS for each given option for point Q

We will apply the distance formula for each given option to calculate QR and QS.

Step 3: Find the total perimeter for each option

We add the distances QR, RS, and QS to get the total perimeter for each option.

Let's start by calculating the exact value of RS, and then we will evaluate the perimeter for each option A, B, C, and D. We will be working with numerical approximations to two decimal places for comparison with the given perimeter of 39.1 units. Let's proceed with the calculations.

The calculations yield the following results:

Step 1: Length of side RS

Using the distance formula, the length of side RS is exactly \( 10\sqrt{2} \), which evaluates to approximately 14.14 units.

Step 2 and 3: Total Perimeter for Each Option

For the given options A, B, C, and D, the total perimeter calculations are as follows:

- Option A: Perimeter ≈ 39.12 units

- Option B: Perimeter ≈ 40.27 units

- Option C: Perimeter ≈ 39.64 units

- Option D: Perimeter ≈ 53.20 units

The perimeter closest to 39.1 units is provided by option A, with a perimeter of approximately 39.12 units.

Therefore, the coordinates of point Q that give triangle QRS a perimeter of approximately 39.1 units are (-12, 15), which corresponds to option A. This is the result after carefully calculating the distance for each option and summing them to find the perimeter that matches the given requirement.