Question

Find an equation of the circle with the following characteristics and sketch its graph.diameter endpoints are (2, 5) and (0, 3)

Answer 1

`(x-1)^2+(y-4)^2=2`

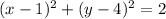
Explanation:

The general equation of a circle, with center (h, k) and radius (r) is:

`\boxed{(x-h)^2+(y-k)^2=r^2}`

To find the equation of a circle whose diameter endpoints are (2, 5) and (0, 3), we first need to find its center (h, k), which is the midpoint of the diameter. To find the midpoint of the diameter, substitute the given diameter endpoints into the midpoint formula.

`\boxed{\begin{array}{l}\underline{\sf Midpoint \;formula}\\\\M(x,y) =\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)\\\\\textsf{where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.}\\\end{array}}`

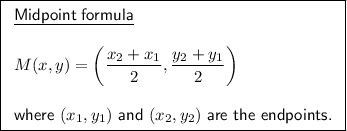
In this case, the diameter endpoints are (2, 5) and (0, 3). Therefore:

`(h,k)=\left((0+2)/(2),(3+5)/(2)\right)`

`(h,k)=\left((2)/(2),(8)/(2)\right)`

`(h,k)=\left(1,4\right)`

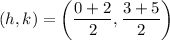
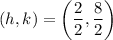
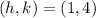
So, the center of the circle is (1, 4).

To find the square of the radius (r²) of the circle, substitute the center (1, 4) and one of the endpoints (0, 3) into the formula for the equation of a circle:

`(0-1)^2+(3-4)^2=r^2`

Solve for r²:

`(-1)^2+(-1)^2=r^2`

`1+1=r^2`

`2=r^2`

`r^2=2`

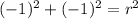
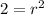
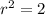
So, the equation of the circle with diameter endpoints (2, 5) and (0, 3) is:

`\large\boxed{\boxed{(x-1)^2+(y-4)^2=2}}`

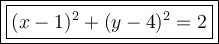
To sketch the graph of the equation of the circle, plot the center at point (1, 4), and both diameter endpoints at (0, 3) and (2, 5). Plot two more points on the circle at (0, 5) and (2, 3). Now, draw a circle with radius √2 that passes through the diameter endpoints and the other plotted points.