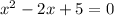The solution set for the quadratic equation
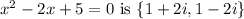 .
.
The given quadratic equation is
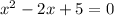 , and we have found the solutions using the quadratic formula:
, and we have found the solutions using the quadratic formula:
![\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]](https://img.qammunity.org/2024/formulas/mathematics/college/n2775bpyhr6nkttp819uth89i6m8ha2p28.png)
In this case,
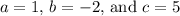 . Substitute these values into the formula:
. Substitute these values into the formula:
![\[ x = (-(-2) \pm √((-2)^2 - 4(1)(5)))/(2(1)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/43mq3p6y2wahfqss4a8ln08pmhxauorylb.png)
Simplify further:
![\[ x = (2 \pm √(4 - 20))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hl2fe5jpqege1xpmgi7516orlv50gj6ozv.png)
![\[ x = (2 \pm √(-16))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6y2vzi1jtiv4wc52yp9gyz5z5svoxea2ys.png)
Since the square root of -16 is an imaginary number
 , we have two complex conjugate solutions:
, we have two complex conjugate solutions:
![\[ x_1 = (2 + 4i)/(2) = 1 + 2i \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x05d8glvfnwsvzusf3r5hhb2siihnjnyo9.png)
![\[ x_2 = (2 - 4i)/(2) = 1 - 2i \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wdkw7yxutmpo7fgv9rkv0s5v753m9hxad0.png)
Complete the question:
What is the solution set of the equation using the quadratic formula?