Question

The average of an electrician's hourly wage and a plumber's hourly wage is $36. One day a contractor hires an electrician for 8hr of work and the plumber for 5hr of work and pays a total of $420 in wages. Find the hourly wage for the electrician and for the plumber.

Answer 1

Answer: The electrician's hourly wage is $20, and the plumber's hourly wage is $52.

Step-by-step explanation:

Step 1: Define the variables.
Let E be the hourly wage of the electrician and P be the hourly wage of the plumber.

Step 2: Write the equations based on the given information.
We are given that the average of the electrician's and plumber's hourly wages is $36. So, we can write the equation:
(E + P) / 2 = 36

We are also given that the contractor hires the electrician for 8 hours and the plumber for 5 hours, and pays a total of $420. So, we can write the equation:
8E + 5P = 420

Step 3: Solve the system of equations.
First, we can solve the first equation for one of the variables. Let's solve for E:
E = 2 * 36 - P
E = 72 - P

Now, substitute this expression for E into the second equation:
8(72 - P) + 5P = 420

Step 4: Simplify and solve for P.
576 - 8P + 5P = 420
-3P = -156
P = 52

Step 5: Substitute the value of P back into the equation for E.
E = 72 - 52
E = 20

So, the hourly wage for the electrician is $20, and the hourly wage for the plumber is $52.

Answer 2

Electrician = $20 per hour

Plumber = $52 per hour

Step-by-step explanation:

To find the hourly wages for both the electrician and the plumber, we can set up a system of equations based on the given information.

Let x be the hourly wage for the electrician (in dollars per hour).

Let y be the hourly wage for the plumber (in dollars per hour).

If the average of an electrician's hourly wage and a plumber's hourly wage is $36, then:

`(x + y)/(2) = 36`

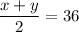
Given a contractor hires an electrician for 8 hours of work and the plumber for 5 hours of work, and pays a total of $420 in wages, then:

`8x + 5y = 420`

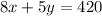
Therefore, the system of equations is:

`\begin{cases}(x + y)/(2) = 36\\\\8x + 5y = 420\end{cases}`

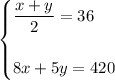
Rearrange the first equation to isolate x:

`\begin{aligned}(x+y)/(2)\cdot 2&=36 \cdot 2\\\\x + y &= 72\\\\x+y-y&=72-y\\\\x &= 72 - y\end{aligned}`

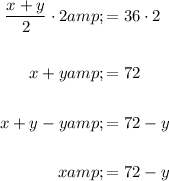
Substitute the expression for x into the second equation and solve for y:

`\begin{aligned}8(72 - y) + 5y &= 420\\\\576 - 8y + 5y &= 420\\\\576 - 3y &= 420\\\\576 - 3y+3y &= 420+3y\\\\576&=420+3y\\\\576-420&=420+3y-420\\\\156 &= 3y\\\\3y&=156\\\\(3y)/(3)&=(156)/(3)\\\\y &= 52\end{aligned}`

Substitute the found value of y into the expression for x and solve for x:

`\begin{aligned}x &= 72 - 52\\\\x &= 20\end{aligned}`

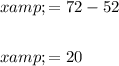
Therefore, the hourly wage for the electrician is $20, and the hourly wage for the plumber is $52.