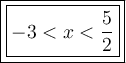Question

Please solve this I can’t do it

Answer 1

`-3 < x < (5)/(2)`

Explanation:

Given inequality:

`2x^2+x-15 < 0`

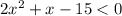
The expression on the left side of the inequality is a quadratic expression with a positive leading coefficient, creating an upward-opening parabola when graphed.

To meet the inequality's requirement of the quadratic being less than zero, we are interested in the region where the parabola is below the x-axis (the values of x between the x-intercepts). Therefore, to solve the given inequality, we need to find the x-intercepts of the quadratic expression.

Factor the quadratic expression on the left side of the inequality.

`2x^2+x-15 < 0`

`2x^2+6x-5x-15 < 0`

`2x(x+3)-5(x+3) < 0`

`(x+3)(2x-5) < 0`

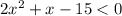
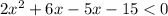
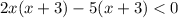
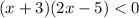
The x-intercepts are the points at which the curve intersects the x-axis, so when y = 0. Therefore, to find the x-intercepts, set each factor equal to zero and solve for x:

`(2x-5)(x+3)=0`

`x+3=0 \implies x=-3`

`2x-5=0 \implies x=(5)/(2)`

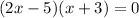
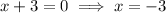
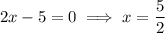
Therefore, the parabola crosses the x-axis at x = -3 and x = 5/2.

Since the parabola opens upwards, the quadratic is negative (less than zero) when the parabola is below the x-axis, which occurs for the x-values between the x-intercepts. Therefore, the solution to the given inequality is:

`\large\boxed{\boxed{-3 < x < (5)/(2)}}`

Answer 2

`(2x - 5)(x+3) < 0`

Explanation:

We can solve the inequality:

`\displaystyle 2x^2+x-15 < 0`

for the variable x by factoring using the grouping method:

First, multiply x's coefficient by the constant term:

`2(-15) = -30`

Then, list out the factor pairs of the product:

-30

(-1, 30)

(-2, 15)

(-3, 10)

(-5, 6)

Select the one whose factors add to the middle x term's coefficient:

-5 + 6 = 1

We can then rewrite the middle x term with these coefficients:

`\displaystyle 2x^2+6x-5x-15 < 0`

We can see that the first two terms and last two terms share common factors of
`2x` and
`-5`, respectively. We can factor (undistribute) these:

`2x(x+3) - 5(x + 3) < 0`

Again, both terms share a common factor of
`(x + 3)`, so we can undistribute that from both terms to form a factored expression:

`\boxed{(2x - 5)(x+3) < 0}`