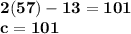Question

The sum of three numbers is 223. The second number is eight more than the first. The third number is thirteen less than twice the first. What are the three numbers?

Answer 1

`\huge\boxed{\bold{a=57}}\\\huge\boxed{\bold{b=65}}}\\\huge\boxed{\bold{c=101}}}`

Explanation:

Let's first see what information is given to determine the values of the three numbers. From the question, we can see that the three numbers add to 223. We can represent this using the terms a,b, and c in the equation
`\bold{a+b+c=223}`.

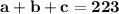We also know that the value of "b" is 8 more than that of "a". The expression
`\bold{a+8}` can represent this. If we are to substitute this back into the primary equation, this would give us
`\bold{a+a+8+c=223}`.

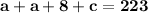From the question, we also know that the value of "c" is 13 less than twice that of "a". We can represent this in terms of a with the expression
`\bold {2a-13}`. By substituting this into the equation, we are then left with
`\bold{a+a+8+2a-13=223}`.

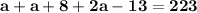We first need to simplify the equation to find the value of "a". This can be done by combining the "a" terms to give us
`\bold{4a-5=223}`. The next step is to isolate the 4a term by adding 5 to both sides, giving us
`\bold{4a=228}`.

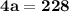The final step in finding the value of "a" is to divide both sides by 4 to give us
`\bold{a=57}`.

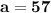Now that we know the value of "a", we can work out the other values. To find the value of "b", we can substitute the value of "a" into the expression a+8 we found earlier, giving us
`\bold{b=65}`.

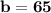The value of "c" can also be found by substituting the value of "a" into the expression 2a-13, giving us
`\bold {c=101}`.

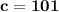Step-by-step calculations:

1) Express the question using the terms a,b, and c.

`\bold{a+b+c=223}`

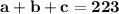
2) Express b in terms of a.

`\bold{b=a+8}`

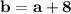
3) Substitute b into the equation.

`\bold{a+a+8+c=223}`

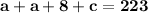
4) Express c in terms of a.

`\bold {c=2a-13}`

5) Substitute c into the equation.

`\bold{a+a+8+2a-13=223}`

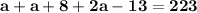
6) Simplify the equation.

`\bold{4a=228}`

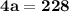
7) Solve for a.

`\bold{a=57}`

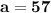
8) Substitute a into the expression for b.

`\bold{(57)+8=65}\\\bold{b=65}`

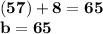
9) Substitute a into the expression for c.

`\bold{2(57)-13=101}\\\bold{c=101}`