Question

A cuboid with a volume of 374 cm^3 has dimensions

2 cm, (x + 3) cm and (x + 9) cm.

Show clearly that x2 + 12x - 160 = 0

Solve the equation by factorisation, making sure you show the factorisation.

State both values of x on the same line.

Finally, find the dimensions of the cuboid, writing all three on one line.​

Answer 1

Explanation:

We have 2(x + 3)(x + 9) = 374.

=> (x + 3)(x + 9) = 187

=> x² + 12x + 27 = 187

=> x² + 12x - 160 = 0. (Shown)

=> (x + 20)(x - 8) = 0

=> x = -20 (rej. as (x + 3) must be positive) or x = 8.

Hence, the dimensions of the cuboid is 2cm x 11cm x 17cm.

Answer 2

Dimensions are: 2 cm, 11 cm and 17 cm

Explanation:

The volume of a cuboid is given by:

Volume = length × width × height

Substituting the given dimensions, we get:

374 = 2 × (x + 3) × (x + 9)

Expanding the right-hand side, we get:

374 =( 2x + 6 ) × (x + 9)

374 = 2x² + 18x + 6x + 54

Subtracting 374 from both sides, we get:

374 - 374= 2x² + 24x + 54 - 374

0 = 2x² + 24x - 320

Taking 2 common in right side

0 = 2 ( x² + 12x - 160 )

Divide both sides by 2, we get:

`\sf x^2 + 12x - 160 = (0)/(2)`

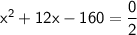
x² + 12x - 160 = 0

Therefore, we can conclude or shown that:

x² + 12x - 160 = 0

Middle term factoring the expression on the left-hand side, we get:

x² + 12x - 160 = 0

x² + 20x - 8x - 160 = 0

Take common from each two terms:

x( x + 20) - 8(x + 20) = 0

Take common again and keep remaining in the bracket.

(x + 20)(x - 8) = 0

Either

x + 20 = 0

x = -20 Neglected because length is always positive

Or

x - 8 = 0

x = 8

Therefore, the value of x is 8.

When we substitute x = - 20 in the above expression, we get

(-20)² + 12×(-20) - 160 = 0

400 - 240 - 160 = 0

0 = 0

and

When x = 8

8² + 12(8) - 160 = 0

64 + 96 - 160 = 0

0 = 0

Since both value satisfy the equation, so

Both values of x are on the same line.

Now, let's find the dimensions of the cuboid:

Substituting the two values of x into the equation:

2 cm

(x + 3) cm = 8 + 3 = 11 cm

(x + 9) cm = 8 + 9 = 17 cm

Therefore, the dimensions of the cuboid are:

2 cm, 11 cm and 17 cm