Question

To start an avalanche on a mountain slope, an artillery shell is fired with an initial velocity of 340 m/s at 56.0° above the horizontal. It explodes on the mountainside 35.0 s after firing. What are the x and y coordinates of the shell where it explodes, relative to its firing point?

Answer 1

Horizontal displacement (
`x`-coordinate): approximately
`6.65 * 10^(3)\; {\rm m}`.

Vertical displacement (
`y`-coordinate): approximately
`3.86 * 10^(3)\; {\rm m}`.

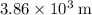Assumption:
`g = 9.81\; {\rm m\cdot s^(-2)}` and air resistance on the projectile is negligible.

Step-by-step explanation:

Under the assumptions, the projectile would travel at a constant horizontal velocity, while accelerating downward with a constant vertical acceleration of
`a_(y) = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}`.

The position of the projectile at the given time
`t = 35.0\; {\rm s}` after launch can be found in the following steps:

• Find initial horizontal and vertical components of velocity,
  `u_(x)` and
  `u_(y)`.
• Apply the SUVAT equation
  `x_(y) = (1/2)\, a_(y)\, t^(2) + u_(y)\, t` to find the vertical displacement
  `x_(y)` (
  `y`-coordinate) of the projectile at the given time.

• Since horizontal velocity of the projectile is constant, find the horizontal position (
  `x`-coordinate) of the projectile at the given time using the equation
  `s = u_(x)\, t`.

Given that the projectile was launched at
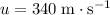`u = 340\; {\rm m\cdot s^(-1)}` at
`\theta = 56.0^(\circ)` above the horizontal, the horizontal and vertical components of initial velocity would be:

Initial horizontal velocity:

`\begin{aligned} u_(x) &= u\, \cos(\theta) \\ &= (340.0\; {\rm m\cdot s^(-1)})\, \cos(56.0^(\circ)) \\ &\approx 190.126\; {\rm m\cdot s^(-1)}\end{aligned}`.

Initial vertical velocity:

`\begin{aligned} u_(y) &= u\, \sin(\theta) \\ &= (340.0\; {\rm m\cdot s^(-1)})\, \sin(56.0^(\circ)) \\ &\approx 281.873\; {\rm m\cdot s^(-1)}\end{aligned}`.

To find the vertical displacement (
`y`-coordinate) of the projectile at the given time, substitute
`a_(y) = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}`,
`t = 35.0\; {\rm s}`, and
`u_(y) \approx 281.873\; {\rm m\cdot s^(-1)}` into the SUVAT equation
`x_(y) = (1/2)\, a_(y)\, t^(2) + u_(y)\, t` :

`\begin{aligned}x_(y) &= (1)/(2)\, a_(y)\, t^(2) + u_(y)\, t \\ &\approx \left[(1)/(2)\, (-9.81)\, (35.0)^(2) + (281.873)\, (35.0)\right]\; {\rm m} \\ &\approx 3.86 * 10^(3)\; \; {\rm m}\end{aligned}`.

(Rounded to three significant figures.)

Since the horizontal velocity of the projectile is constant, horizontal displacement (coordinate) of the projectile can be found using the equation
`s = u_(x)\, t`:

`\begin{aligned}s &= u_(x)\, t \\ &\approx (190.126)\, (35.0)\; {\rm m} \\ &\approx 6.65 * 10^(3)\; {\rm m}\end{aligned}`.

(Rounded to three significant figures.)