Question

PLEASE it’s due tomorrow help

Answer 1

29) m∠G = 61°

30) m∠D = 34°

31) m∠FWV = 110°

32) m∠S = 18°

Explanation:

To find the measures of the indicated angles, we can use the Exterior Angle Theorem to first find the value of x, then substitute this into the angle expression.

The Exterior Angle Theorem states that the exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles of the triangle.

`\hrulefill`

Question 29

Find the value of x by setting the exterior angle ∠SFG to the sum of the two non-adjacent interior angles ∠G and ∠H:

`\begin{aligned}7x+17&=6x-5+33\\7x+17&=6x+28\\7x+17-6x&=6x+28-6x\\x+17&=28\\x+17-17&=28-17\\x&=11\end{aligned}`

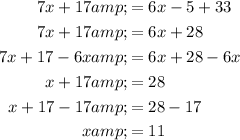
Now, substitute the found value of x into the angle expression for ∠G:

`\begin{aligned}m \angle G&=6(11)-5\\m \angle G&=66-5\\m \angle G&=61^(\circ)\end{aligned}`

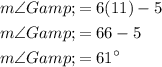
Therefore, m∠G = 61°.

`\hrulefill`

Question 30

Find the value of x by setting the exterior angle ∠QBC to the sum of the two non-adjacent interior angles ∠D and ∠C:

`\begin{aligned}120&=5x-6+10x+6\\\\120&=15x\\\\15x&=120\\\\(15x)/(15)&=(120)/(15)\\\\x&=8\end{aligned}`

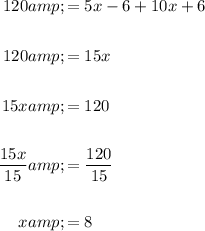
Now, substitute the found value of x into the angle expression for ∠D:

`\begin{aligned}m \angle D&=5(8)-6\\m \angle D&=40-6\\m \angle D&=34^(\circ)\end{aligned}`

Therefore, m∠D = 34°.

`\hrulefill`

Question 31

Find the value of x by setting the exterior angle ∠FWV to the sum of the two non-adjacent interior angles ∠U and ∠V:

`\begin{aligned}15x+5&=70+4x+12\\15x+5&=4x+82\\15x+5-4x&=4x+82-4x\\11x+5&=82\\11x+5-5&=82-5\\11x&=77\\x&=7\end{aligned}`

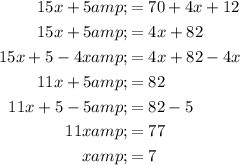
Now, substitute the found value of x into the angle expression for ∠FWV:

`\begin{aligned}m \angle FWV&=15(7)+5\\m \angle FWV&=105+5\\m \angle FWV&=110^(\circ)\end{aligned}`

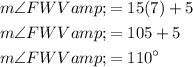
Therefore, m∠FWV = 110°.

`\hrulefill`

Question 32

Find the value of x by setting the exterior angle ∠ZRS to the sum of the two non-adjacent interior angles ∠T and ∠S:

`\begin{aligned}73&=7x+6+x+11\\73&=8x+17\\73-17&=8x+17-17\\56&=8x\\8x&=56\\x&=7\end{aligned}`

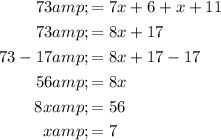
Now, substitute the found value of x into the angle expression for ∠S:

`\begin{aligned}m \angle S&=7+11\\m \angle S&=18^(\circ)\end{aligned}`

Therefore, m∠S = 18°.