Question

Calculate the area of the shaded region.

Answer 1

234cm²

Explanation:

Area of a Trapezoid =
`(h(b_1+b_2))/(2)` ;

h=height perpendicular to the parallel bases

b₁ and b₂ are the lengths of the parallel lines

1. Calculate the Area of the larger (outer) trapezoid:

`A=(22(14+25))/(2) =(22(39))/(2)=11(39)=429`cm²

2. Calculate the Area of the smaller (inner/not shaded) trapezoid:

`A=(10(8+25))/(2) =(10(33))/(2)=5(39)=195`cm²

3. Subtract the smaller from the larger:

Area of shaded region = (429-195)cm²

**Remember to include units!!**

I hope this helps!

Answer 2

264 cm²

Explanation:

The area of a trapezoid is calculated using the following formula:

`\sf Area = (1)/(2) (base1 + base2) * height`

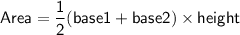
where:

• base1 and base2 are the lengths of the parallel sides of the trapezoid
• height is the perpendicular distance between the two bases

In this case we do have two trapezoid.

So,

For Big Trapezoid:

• Base 1 = 14 cm
• Base 2 = 25 cm
• Height = 10 cm + 12 cm = 22 cm

Substituting these value in above formula:

`\sf \textsf{ Area of big Trapezoid} = (1)/(2) (14+25)(22) \\\\ \sf 429 cm^2`

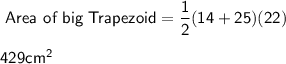
Similarly:

For small Trapezoid:

• Base 1 = 8 cm
• Base 2 = 25 cm
• Height = 10 cm

Substituting these value in above formula:

`\sf \textsf{ Area of big Trapezoid} = (1)/(2) (25+8)(10) \\\\ \sf = 165cm^2`

We can find the area of the shaded region by subtracting the small Trapezoid from a big Trapezoid.

Area of shaded region = 429cm² - 165cm²

Area of shaded region = 264 cm²

Therefore, the area of the shaded region is 264 cm².