Question

A horizontal force, F1 = 95 N, and a force, F2 = 18.6 N acting at an angle of θ with respect to the x-axis, as shown, are applied to a block of mass m = 2.3 kg. The coefficient of kinetic friction between the block and the surface is μk = 0.2. The block is moving to the right. Solve numerically for the magnitude of acceleration of the block, a in m/s2, if θ = 30°.

Answer 1

Answer: A. 13.26 N; B. 47.17 m/s²

Step-by-step explanation:
Theory:

Newton's second rule can be expressed as F = ma, which means the force (F) exerted on an object is equal to its mass (m) multiplied by its acceleration (a).

For an object to be in equilibrium, the total external force acting on the object must be zero. As such, the forces acting along each axis of motion must sum to zero:

`\sum \mathbf{F}_x + \sum \mathbf{F}_y = 0`

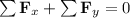
Given:

Coefficient of kinetic friction: μk = 0.2

Angle made by the forces: θ1 = 0° and θ2 = 30°

External force magnitudes: F1 = 95 N and F2 = 18.6 N

Mass of the block: 2.3 kg

A. Along the vertical direction:

`\begin{align} \sum F_y=ma \\[2ex] N \ + \ F_2 * \sin \theta_2 \ &= \ M * g \\[2ex] N \ + \ 18.4 * \sin 30^\circ \ &= \ 2.1 * 9.8 \\[2ex] \implies \ N \ &= \ 11.38 \ N \end{align}`
`\sum F_y=ma \\[2ex] N \ + \ F_2 * \sin \theta_2 \ = \ M * g \\[2ex] N \ + \ 18.6 * \sin 30^\circ \ = \ 2.3 * 9.81 \\[2ex] \arrow\ N \ = \ 13.26 \ N`

B. The block's kinetic frictional force is as follows:

`f_k \ = \ \mu * N \\[2ex] = \ 0.2 * 13.26 \\[2ex] f_k \ = 2.652 \ N`

Note: The positive answer indicates that the force operates in the opposite direction of motion.

Using Newton's 2nd Law, where α is the acceleration of the block:

`\sum F_x=ma \\[2ex] F_1 \ + \ F_2 * \cos \theta \ - \ f_k=Ma \\[2ex] a \ = \ (F_1 \ + \ F_2 * \cos \theta \ - \ f_k)/(M) \\[2ex] = \ (95\ + \ 18.64 * \cos 30^\circ \ - \ 2.652)/(2.3) \\[2ex] a \approx \ 47.17 \ \text{m/s}^2`