Question

If f(x) = 2x^3 + Ax^2 +4x -5 and f(2)=5, then what is the value of A?

Answer 1

`(-7)/(2)`

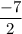
Explanation:

Here we are given a polynomial ,

`\implies f(x) = 2x^3 + Ax^2 + 4x - 5`

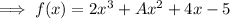
And the value of ,

`\implies f(2) = 5 \dots (i)`

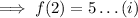
And we need to find out the value of A . Firstly substitute x = 2 in f(x) , we have ,

`\implies f(2) = 2(2)^3+ A(2)^2 + 4(2) -5`

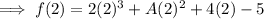
Simplify the exponents ,

`\implies f(2) = 2(8) + A(4) + 8 - 5`

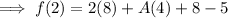
Simplify by multiplying ,

`\implies f(2) = 16 + 4A + 3`

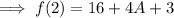
Add the constants ,

`\implies f(2) = 19 + 4A`

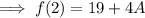
Now from equation (i) , we have ,

`\implies 19 + 4A = 5`

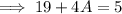
Subtracting 19 both sides,

`\implies 4A = 5-19`

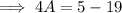
Simplify,

`\implies 4A = -14`

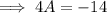
Divide both sides by 4 ,

`\implies A =(-14)/(4)=\boxed{ (-7)/(2)}`

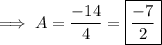
Hence the value of A is -7/2.