Answer:
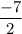
Explanation:
Here we are given a polynomial ,
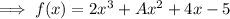
And the value of ,
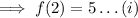
And we need to find out the value of A . Firstly substitute x = 2 in f(x) , we have ,
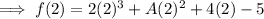
Simplify the exponents ,
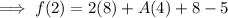
Simplify by multiplying ,
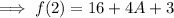
Add the constants ,
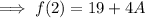
Now from equation (i) , we have ,
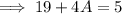
Subtracting 19 both sides,
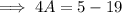
Simplify,
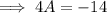
Divide both sides by 4 ,
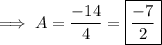
Hence the value of A is -7/2.