Question

A manufacturer finds that the revenue generated by selling x units of a certain commodity is given by the function

R(x)= 100x - 0.2x²,
where the revenue R(x) is measured in dollars.

What is the maximum revenue, and how many units should be manufactured to obtain this maximum?

Answer 1

250 units manufactured for maximum revenue

Maximum Revenue Generated: $12500

Explanation:

R'(x) = 0 gives us the maximum value for revenue

Differentiating the expression (using the power rule) gives us R'(x)

`R'(x) = 100 - 2(0.2)x^2^-^1\\R'(x) = 100 - 0.4x\\100 -0.4x = 0\\0.4x = 100\\x = 250`

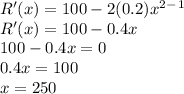
250 units are needed to generate maximum revenue

Substitute 250 back into R(x) to find the maximum revenue in dollars

R(250) = 100(250) - 0.2(250)²

R(250) = 12500

Maximum revenue is $12500