Question

Use the dimensions (length and width) of the area model at right to write the area as a product of the dimensions equal to the area as the sum of the parts. -x +y +2 x -4

Answer 1

The area of a rectangle is given by the product of its length and width. In this case, the dimensions of the rectangle are given as `-x + y + 2` and `x - 4`. Therefore, the area of the rectangle can be written as the product of these dimensions:

`$$(-x + y + 2)(x - 4)$$`

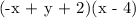
This product can be expanded to give the area as the sum of its parts:

`$$-x^2 + 4x + xy - 4y + 2x - 8$$\\`

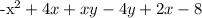
Simplifying this gives:

`$$-x^2 + (4 + y)x - 4y - 8$$`

So, the area of the rectangle can be written as either the product of its dimensions `(-x + y + 2)(x - 4)` or as the sum of its parts `-x^2 + (4 + y)x - 4y - 8`. Both expressions represent the same quantity, but in different forms.