Question

Given the function defined in the table below, find the average rate of change, in simplest form, of the function over the interval 2, is less than or equal to, x, is less than or equal to, 2 ≤ x ≤ 8.

x f(x)
0 78
2 70
4 62
6 54
8 46
10 38

Answer 1

AvgROC = -11/3

Explanation:

Average rate of change between x = 2 and x = 8

`AvgROC = (y_(2) - y_(1) )/(x_(2) - 1_(1)) = (46 - 70)/(8 - 2) = -(11)/(3) or-3.667`

Answer 2

Answer: -4

Explanation

The average rate of change is the same as the slope of the line through the indicated endpoints.

When x = 2, y = f(x) = 70 based on the table. In other words, f(2) = 70.

When x = 8, y = f(x) = 46.

The two points we're going to focus on are (2,70) and (8,46).

Let's find the slope of the line through these points.

`(x_1,y_1) = (2,70) \text{ and } (x_2,y_2) = (8,46)\\\\m = \text{slope} = \frac{\text{rise}}{\text{run}} = \frac{\text{change in y}}{\text{change in x}}\\\\m = \frac{\text{y}_(2) - \text{y}_(1)}{\text{x}_(2) - \text{x}_(1)}\\\\m = (46 - 70)/(8 - 2)\\\\m = (-24)/(6)\\\\m = -4\\\\`

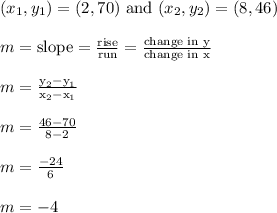
Therefore, the average rate of change is -4.