Question

Determine the value of x for the following isosceles triangle.

Answer 1

Given :

▪︎This triangle is an isosceles triangle.

▪︎Measure of one of its legs = 6 inches

▪︎Measure of its equivalent leg
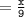`= \tt (x)/(9)` inches

▪︎Measure of its base
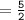`= \tt (5)/(2)` inches

Which means :

`=\tt 6 = (x)/(9)`

`=\tt (6)/(1) = (x)/(9)`

`=\tt 6 * 9 = x * 1`

`\hookrightarrow\color{plum}\tt 54 = x`

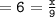
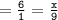
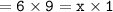
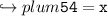
Let us check whether or not we have found out the correct value of x by placing 54 in the place of x :

`=\tt 6 = (54)/(9)`

`= \tt6 = 6`

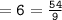
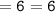
Since the Left Hand Side of the equation is equivalent to the Right Hand Side of the equation, we can conclude that we have found out the correct value of x.

▪︎Therefore, the value of x = 54