Question

a ball is thrown vertically upward with a speed of 31.0 m/s. (a) how high does it rise? m (b) how long does it take to reach its highest point? s (c) how long does the ball take to hit the ground after it reaches its highest point? s (d) what is its velocity when it returns to the level from which it started? m/s

Answer 1

(a) Approximately
`49.0\; {\rm m}`.

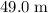(b) Approximately
`3.16\; {\rm s}`.

(c) Approximately
`3.16\; {\rm s}`.

(d)
`31.0\; {\rm m\cdot s^(-1)}`, downwards.

Assumptions: air resistance on the ball is negligible, the ball was on the ground when it was launched, and that
`g = 9.81\; {\rm m\cdot s^(-2)}`.

Step-by-step explanation:

Under the assumptions, the ball would be accelerating on the influence of its weight. The acceleration of the ball would be constantly
`a = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}` (negative since the gravitational attraction on the ball points dowards.)

(a)

When the ball is at the maximum height, velocity of the ball would be
`v = 0\; {\rm m\cdot s^(-1)}`.

The initial velocity of the ball is
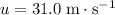`u = 31.0\; {\rm m\cdot s^(-1)}`. Apply the SUVAT equation
`v^(2) - u^(2) = 2\, a\, x` to find the displacement
`x` of this ball by the time it reached maximum height. Rearrange this equation to obtain:

`\begin{aligned}x &= (v^(2) - u^(2))/(2\, a) \\ &= ((0)^(2) - (31.0)^(2))/(2\, (-9.81)) \; {\rm m} \\ &\approx 49.0\; {\rm m}\end{aligned}`.

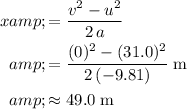In other words, at the vertex of the trajectory, this ball would be approximately
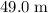`49.0\; {\rm m}` above where it was launched.

(b)

Divide the change in the velocity by acceleration (rate of change in velocity) to find the time required:

`\begin{aligned}t &= (v - u)/(a) \\ &= (0 - 31.0)/((-9.81))\; {\rm s} \\ &\approx 3.16\; {\rm s}\end{aligned}`.

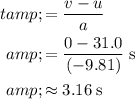In other words, it would take approximately
`3.16\; {\rm s}` for the ball to reach its maximum height.

(c)

The time required for the ball to return to its initial height is the same as the time required for the ball to reach maximum height after launch.

Assuming that the ball in this question was on the ground when it was launched. The time required to return to this position from the maximum height would be the same as the time required for to reach maximum height after launch- approximately
`3.16\; {\rm s}`.

(d)

The velocity of the ball right before landing would have the same magnitude as the velocity at launch, but in the opposite direction. Since the initial velocity of this ball was
`31.0\; {\rm m\cdot s^(-1)}` upward, the velocity right before landing would be
`31.0\; {\rm m\cdot s^(-1)}\!` downward.