Question

Quadrilateral ABCD is a rectangle. Find BD if AO = 6x - 22 and OC = 2x + 6.

A) 7 units



B) 20 units



C) 10 units



D) 40 units

Answer 1

D) 40 units

Explanation:

In a rectangle, the diagonals are equal in length and also bisect each other. Therefore, in rectangle ABCD:

`\overline{AC} = \overline{BD}\;\;\textsf{and}\;\;\overline{AO} = \overline{BO} = \overline{OC} = \overline{OD}`

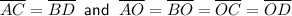
To find the length of BD, first find the value of x by setting the expressions for AO and OC equal to other and solving for x:

`\begin{aligned}\overline{AO}&=\overline{OC}\\6x-22&=2x+6\\6x-22-2x&=2x+6-2x\\4x-22&=6\\4x-22+22&=6+22\\4x&=28\\4x / 4&=28 / 4\\x&=7\end{aligned}`

Substitute the found value of x into the expression for AO:

`\begin{aligned}\overline{AO}&=6(7)-22\\\overline{AO}&=42-22\\\overline{AO}&=20\end{aligned}`

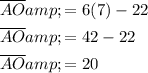
BD is the sum of BO and OD.

Since BO = OD = AO = 20, then:

`\begin{aligned}\overline{BD}&=\overline{BO}+\overline{OD}\\\overline{BD}&=20+20\\\overline{BD}&=40\end{aligned}`

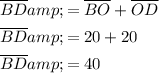
Therefore, the length of diagonal BD is 40 units.