Question

The position of a particle moving along the y axis has a position given by y= 0.20m + (8.0 m/s)t- (10 m/s^2)t^2. Is there any time interval during which the particle is not moving.

Answer 1

The particle is moving at all time except at
`t = 0.4\; {\rm s}`.

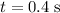Step-by-step explanation:

The particle is not moving if and only if the velocity of this particle is
`0`.

Given the position of this particle as a function of time. The velocity function of this function can be found by differentiating the position function with respect to time:

`\begin{aligned} v(t) &= (d)/(dt)\left[y(t)\right] \\ &= (d)/(dt)\left[0.20 + 8.0\, t - 10\, t^(2)\right] \\ &= 8.0 - 20\, t\end{aligned}`.

Set the value of
`v(t)` to
`0` and solve for
`t` to moments when the particle isn't moving:

`v(t) = 0`.

`8.0 - 20\, t = 0`.

`\displaystyle t = (8.0)/(20) \; {\rm s}= 0.4\; {\rm s}`.

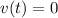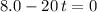In other words, the particle would be moving at all time except at
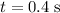`t = 0.4\; {\rm s}`.